|
Практические, проверочные и
домашние работы
 rtf
Домашняя работа "Системы счисления" |
Как только
люди стали общаться, т.е. передавать информацию, они стали
считать. Первыми инструментами счета были пальцы рук и простые
предметы, например, камешки. Слово "камешки" по латыни CALCULI, а их
перебрасывание при счете - CALCULARE, что и означает "считать". Отсюда -
"калькулятор".
Затем расчеты стали фиксировать, что привело к появлению систем
счисления.
Система счисления - это свод приемов
обозначения и записи чисел при помощи специальных символов - цифр.
Сначала люди придумали непозиционные или
кодовые системы счисления (IV тысячелетие до н.э.), в которых
расположение цифр в числе не имеет значения и для обозначения каждого
числа существует свой символ. Пример такой системы - египетская:
Но в непозиционных системах трудно записывать большие числа и выполнять
арифметические действия. Более совершенной системой (переходной от
непозиционных систем к позиционным) стала - римская (500 лет до н.э.),
которая применяется и в наше время. Алфавитом (цифрами) этой системы
служат символы:
I (1)
V (5)
X (10)
L (50)
C (100)
D (500)
M (1000)
Здесь уже положение цифры в числе меняет ее значение. Например, в числе
IV I отнимается от V, а в числе
VI - прибавляется к V. Число 1995 в этой системе запишется так:
MCMXCV.
Но и этой системе присущи все недостатки непозиционных систем. Чтобы от
них избавиться понадобились позиционные системы.
Если место, занимаемое символом в записи числа,
придает этому символу определенное значение, то такая система счисления
называется
позиционной.
Количество цифр системы (символов алфавита)
называется ее
основанием, место цифры в числе - разрядом, а количество
цифр в числе - его
разрядностью.
Самой древней известной позиционной системой счисления считают
вавилонскую шестидесятеричную. Следы ее сохранились до наших дней в
единицах измерения времени и угловых величин. Но наибольшее
распространение получила и имеет до сих пор индо-арабская ДЕСЯТИЧНАЯ
СИСТЕМА (VI в). Возможно, она наиболее естественна для человека, т.к.
считать мы учимся на пальцах, а их на двух руках как раз 10. В этой
системе 10 цифр: от 0 до 9. Каждая цифра в числе при перемещении справа
налево в следующий разряд увеличивает свое значение в 10 раз.
Любое число может быть представлено в виде суммы, где каждое слагаемое
представляет собой произведение коэффициента (цифры числа) на основание
системы (10) в степени, равной разряду этой цифры. Посмотри внимательно
на пример внизу и прочитай еще раз предыдущее предложение:
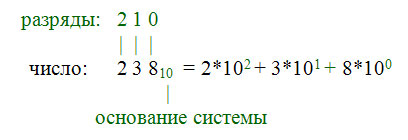
Итак,
основание системы счисления - это количество цифр (символов алфавита) в
ней. Какое число можно принять за основание системы? Любое натуральное,
например, 1. В этом случае мы получаем унарную систему счисления,
древнейшую в истории культуры счета. В ней для записи чисел применяется
только один символ (камешек, палочка, зарубка). Число в ней - это
количество таких символов.
Нас же будет интересовать двоичная (бинарная) система счисления, в
которой работают все ЭВМ. (На самом деле существовала одна-единственная
ЭВМ "Сетунь", разработанная в МГУ конструктором
Н.П. Брусенцовым, которая работала в троичной системе счисления. Ее
создатели доказали, что применение этой системы наиболее экономично с
точки зрения использования аппаратурных средств, но последователей у них
не было).
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Представьте себе счеты, у которых на каждой проволочке не 10, а 2
косточки. Попробуем на таких счетах отложить числа 1, 2, 3 и 4:
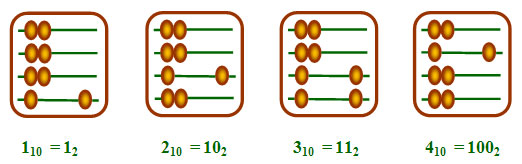
Индекс
внизу - основание системы счисления. Все числа в двоичной системе
записываются с помощью двух цифр: 0 и 1. Подобно тому, как мы
раскладывали любое десятичное число по степеням десятки, разложим
двоичное число по степеням двойки:
Мы
получили способ перевода из двоичной системы счисления в десятичную. А
как решить обратную задачу перевода десятичного числа в двоичное? Для
этого нужно последовательно делить заданное число на 2 и выписывать
остатки от каждого деления. Перевод числа 25 в двоичную систему:
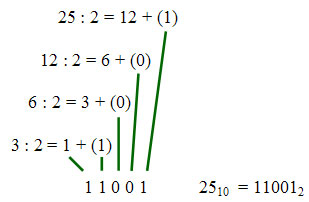
Деление
продолжается до тех пор, пока частное не станет меньше двух (т.е. 1).
Первая цифра результата - последнее частное (1), следующие цифры -
остатки, взятые в обратном порядке. 
|
Приложения
Задачник-практикум (Т. 1),
1.5.1-1.5.2 [4]
pdf
Презентация "История счёта и
систем счисления"
(Л.Л. Босова)
"Представление числовой
информации с помощью систем счисления"
(В.Н. Кучинская, Новосибирская обл.)
pdf
Презентация "Системы счисления"
(Н.М. Попушанская, г. Петропавловск-Камчатский)
Вопросы по теме "Системы счисления" |
