Практические, проверочные и домашние работы

exe Тест "Системы счисления"
(Е.В. Грязнова, п.г.т. Мама)

rtf Домашняя работа "Разные системы счисления"

Основанием позиционной системы счисления может быть любое натуральное число. Например, вы можете работать в шестеричной системе, тогда в ней должно быть 6 цифр (символов алфавита): 0, 1, 2, 3, 4, 5. Чтобы перевести какое-нибудь число (например, 235) из этой системы в десятичную, нам нужно разложить его по степеням шестерки (основания системы): 235₆ = 5×6⁰ + 3×6¹ +2×6² = 5 + 18 + 72 = 95₁₀ А чтобы перевести число из десятичной системы в шестеричную, нужно делить это число на 6 (на основание системы счисления) с остатками:
95 : 6 = 15 (5)
15 : 6 = 2 (3)
95₁₀ = 235₆
Аналогично и в любых других системах счисления. В программировании часто используются восьмеричная и шестнадцатеричная системы счисления. Рассмотрим их подробнее. В восьмеричной системе должно быть 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Попробуем перевести число, например 137, из восьмеричной системы в десятичную: 137₈ = 7×8⁰ + 3×8¹ + 1×8² = 7 + 24 + 64 = 95₁₀
Теперь наоборот, число 76 из десятичной системы в восьмеричную:
76 : 8 = 9 (4)
9 : 8 = 1 (1)
76₁₀ = 114₈

Приложения

Задачник-практикум (Т. 1), 1.5.3 [4]

pdf Презентация
"Системы счисления"
(Е.В. Грязнова, п.г.т. Мама)

pdf Презентация "Цифровые данные"
(Л.Л. Босова)

Учебник по теме "Системы счисления" (рук. Л.Л. Сороко, г. Болотное, НСО)

А можно ли перейти из восьмеричной системы в двоичную? Казалось бы придется переходить сначала из восьмеричной в десятичную, а потом уже из десятичной в двоичную. Но оказывается есть более простой способ. Сначала каждое число, соответствующее цифре восьмеричной системы, представим в виде трехразрядного двоичного кода (переведем в двоичную систему).
Теперь правило: чтобы перевести число из восьмеричной системы в двоичную, надо каждую его цифру заменить на соответствующую тройку цифр (двоичный код).
Например, переведем восьмеричное число 351 в двоичное:
351₈= 011 101 001 = 11101001₂

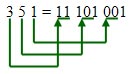Для перевода двоичного числа в восьмеричное надо наоборот, разбить исходное число на тройки цифр, начиная с конца, и заменить каждую тройку на соответствующую ей цифру восьмеричной системы.
Например, переведем двоичное число 11100110 в восьмеричное:
11100110₂ = 011 100 110 = 346₈

Теперь рассмотрим шестнадцатеричную систему счисления. Как Вы понимаете, в ней должно быть 16 цифр. Обозначение первых десяти можно взять из десятичной системы счисления, а для остальных шести решили использовать первые шесть букв латинского алфавита: 10 - A,  11 - B,   12 - C,   13 - D,   14 - E,   15 - F.
Переведём число А1F8 из шестнадцатеричной системы в десятичную:
А1F8₁₆ = 8×16⁰ + 15×16¹ + 1×16² + 10×16³ = 8 + 240 + 256 + 40960 = 41464₁₀
В обратную сторону: число 196 из десятичной системы в шестнадцатеричную:
196 : 16 = 12 (4) , т.е. 196₁₀ = С4₁₆
А есть ли простая связь между числами двоичной и шестнадцатеричной систем? Оказывается, есть и аналогична связи между числами двоичной и восьмеричной систем.
Опять запишем каждое число, соответствующее цифре шестнадцатеричной системы в виде двоичного кода, только теперь четырехразрядного:
Теперь для перевода числа из шестнадцатеричной системы в двоичную надо каждую его цифру заменить на соответствующую четверку двоичных цифр. А как перевести двоичное число в шестнадцатеричное вы, наверное, уже сообразили сами.